The NANOGrav 11-year Data Set:
Pulsar-Timing Constraints on the Stochastic Gravitational-Wave Background
by the NANOGrav Collaboration; corresponding author: Stephen R. Taylor.
Published in The Astrophysical Journal, May 23rd 2018.
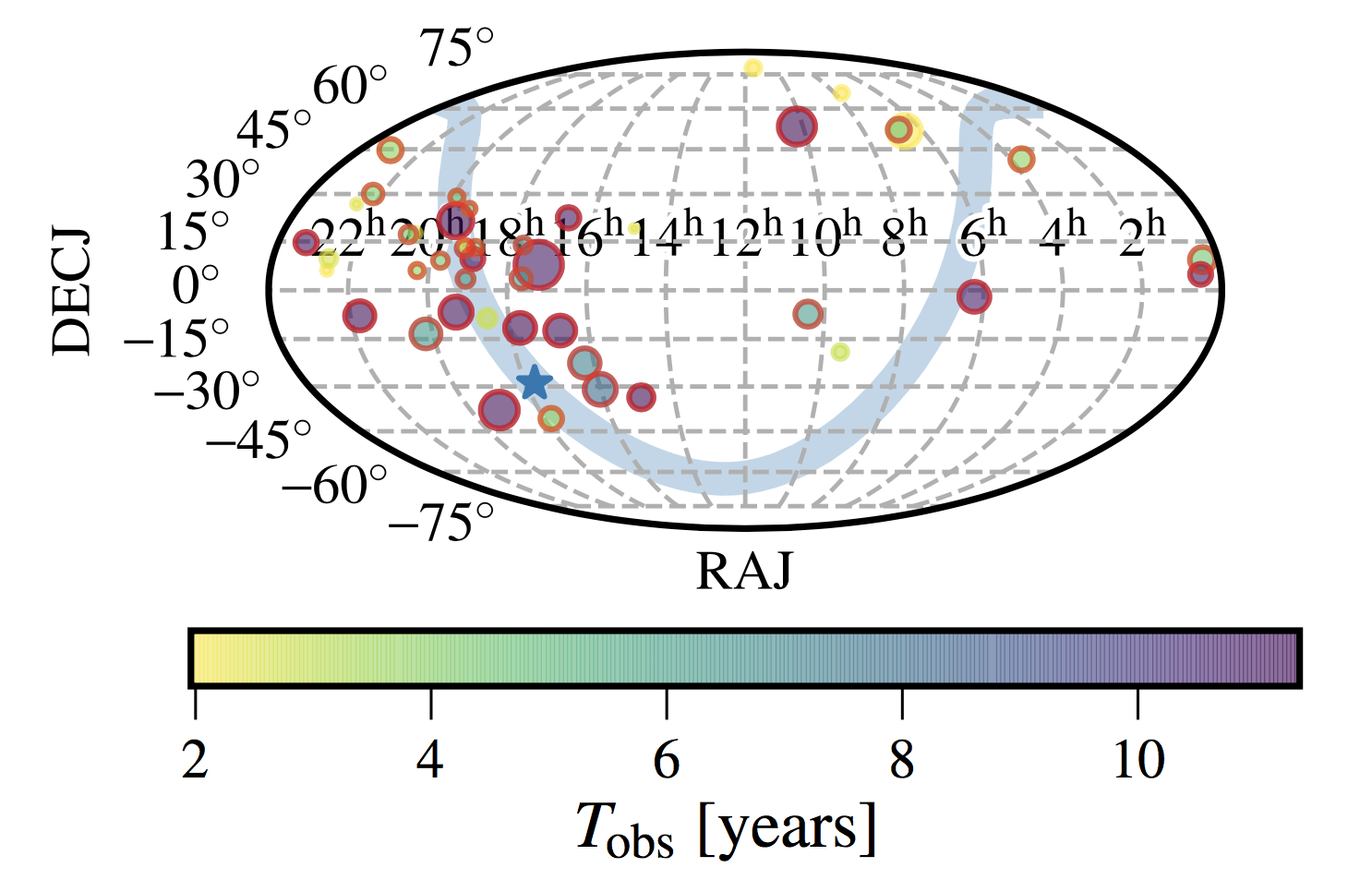
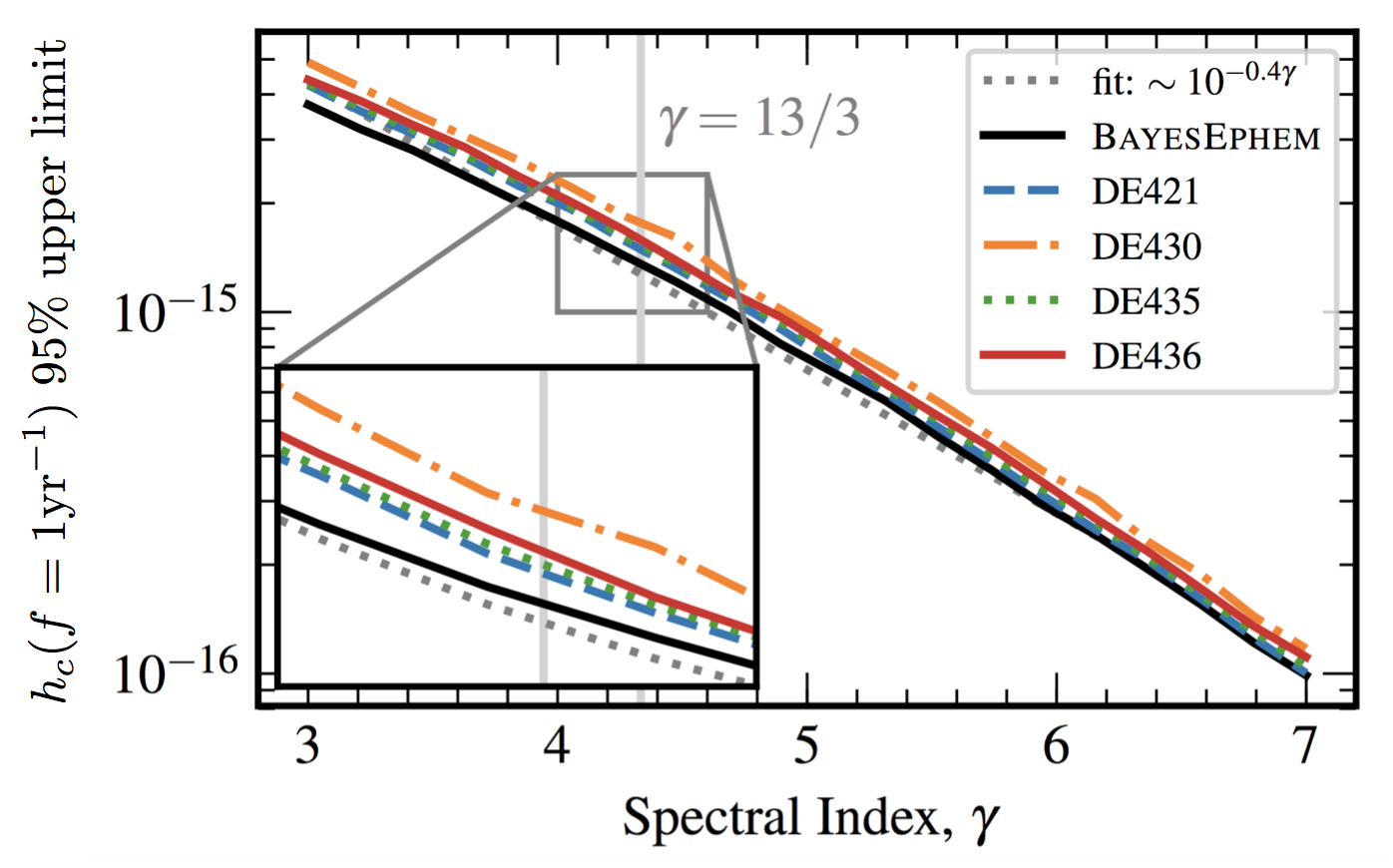
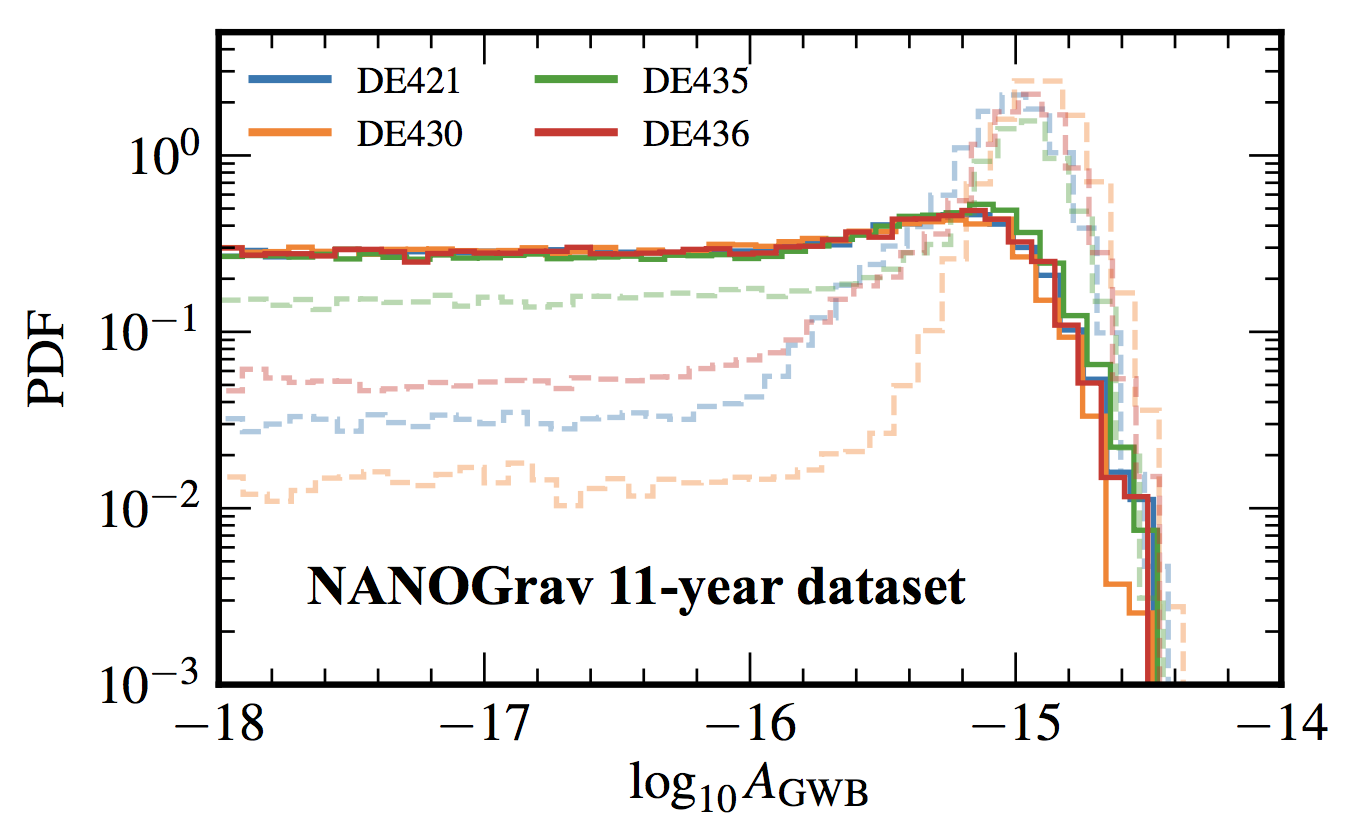
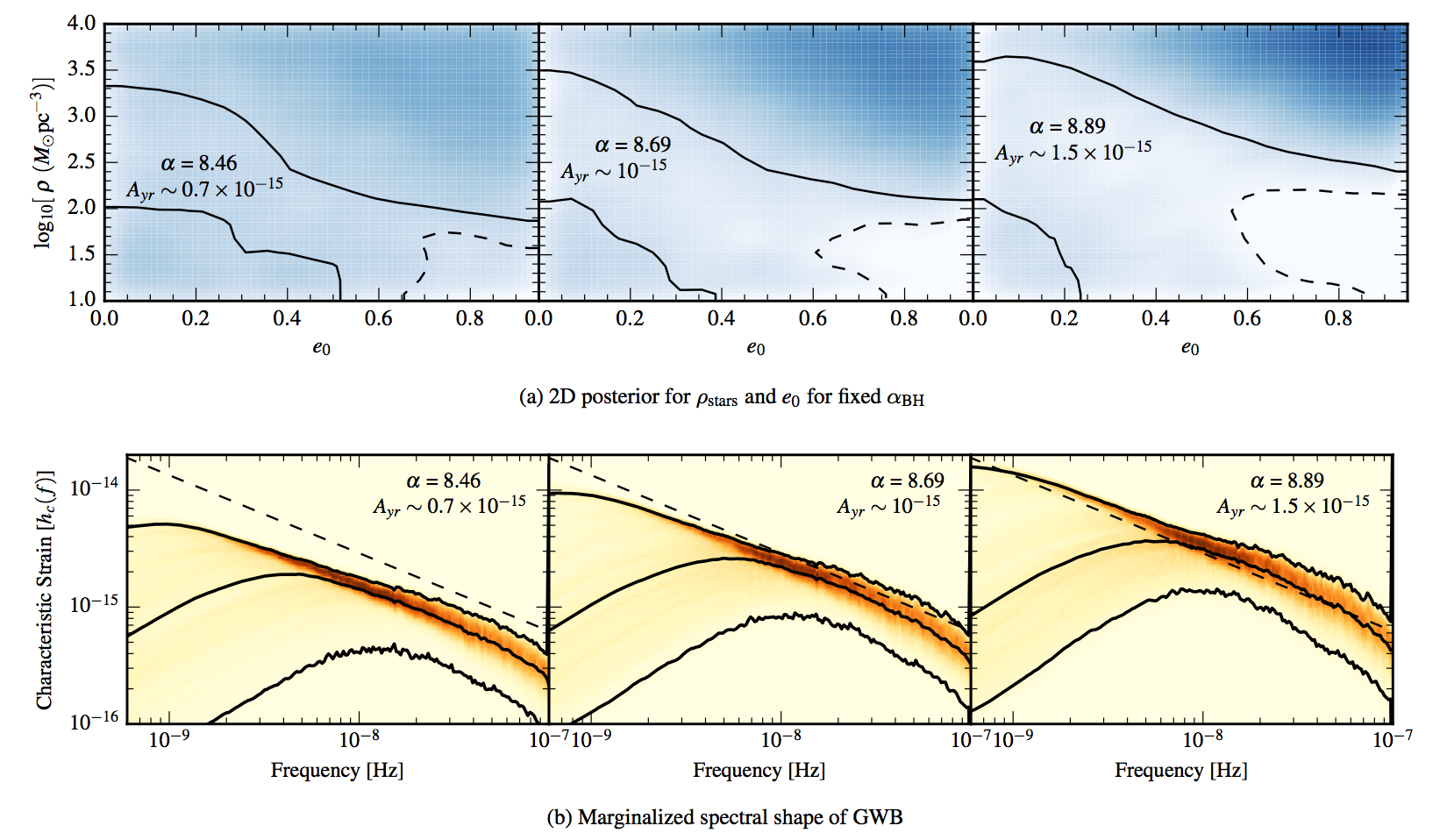
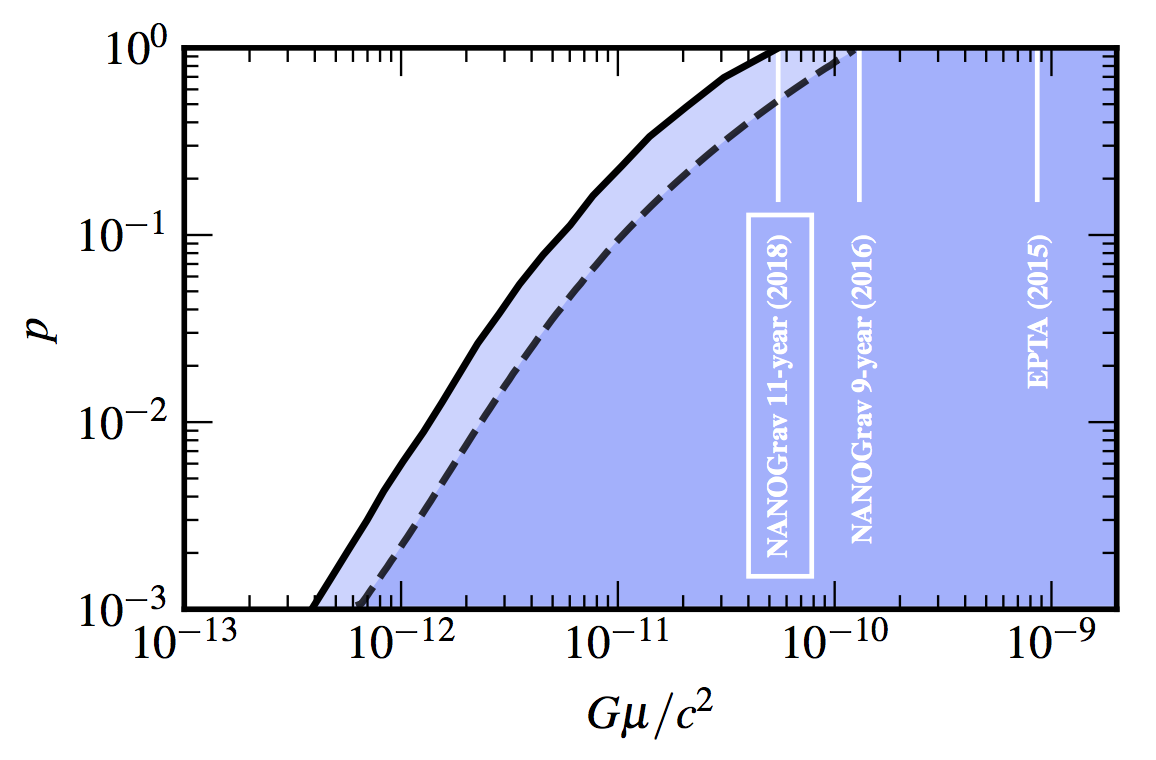
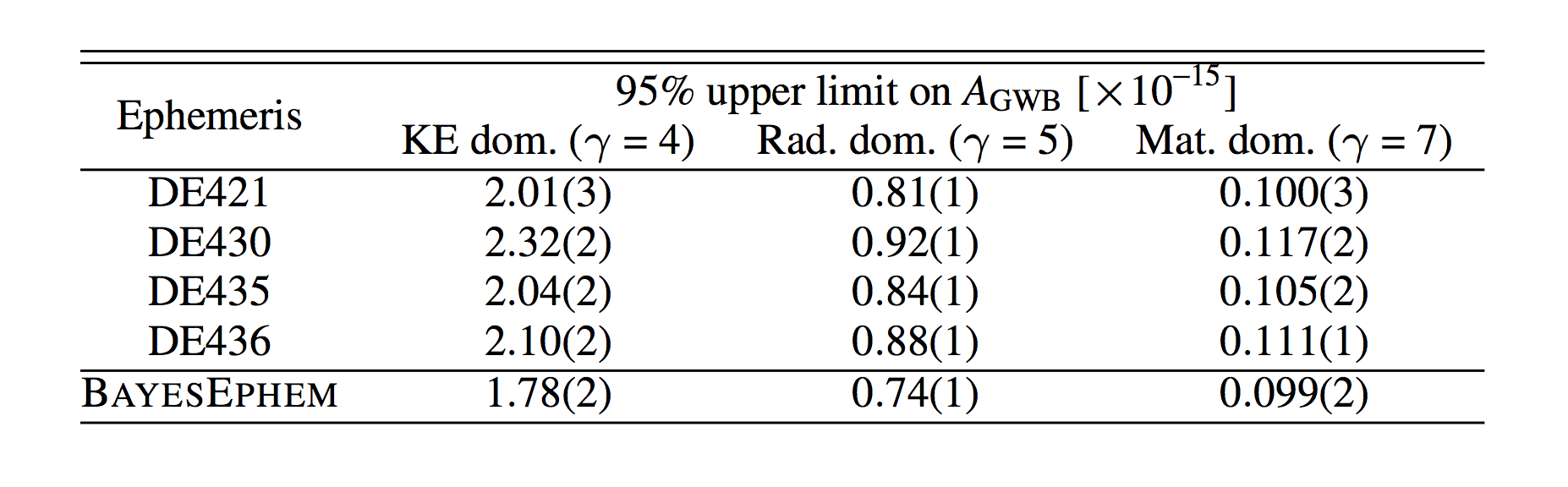
We search for a gravitational-wave background (GWB) in the newly released 11-year dataset from the North American Nanohertz Observatory for Gravitational Waves (NANOGrav). While we find no significant evidence for a GWB, we place new constraints on a GWB from a population of inspiraling supermassive black-hole binaries, from a network of cosmic strings, and from a primordial GWB. For the first time, we find that the GWB upper limits and detection statistics are sensitive to the Solar-System ephemeris (SSE) model that we assume, and that SSE errors can mimic a GWB signal. We develop and implement a novel approach to model SSE errors, producing the first pulsar-timing GWB constraints that are robust against SSE uncertainties. In keeping with the principles of open science, we release the source code and data for our analysis, as well as a Docker image that can be used to reproduce it.